在磁性液體密封的理論及現有設計原則的基礎上,建立了以磁鐵體積最小和極靴長度最小為目標的密封結構優化設計的數學模型。利用帶有約束條件的多目標混合遺傳算法,通過Matlab 編程與Ansys 軟件的交互運算,實現了對密封結構的優化設計。結合具體實例的計算結果并與初始值的比較表明,在保證密封耐壓的前提下,優化后的結構參數可以使磁鐵體積減小74.7 % ,極靴長度減小5.45 % ,漏磁減小84.5 %。

　　磁性液體密封的設計通常以耐壓能力為主要設計目標,而耐壓能力取決于密封間隙內的磁場和磁性液體的磁化特性。密封結構與參數對密封間隙內磁場有決定性影響,如何在給定密封耐壓下最優設計密封結構尺寸,以減小其體積,降低密封裝置成本,是現今密封裝置設計的重要問題。Oscar Pinkus等在理論推導和實驗總結的基礎上給出了部分結構尺寸的選定范圍,但這對總體結構尺寸的確定尚不全面。鄒繼斌、趙國偉等從材料選取和結構設計方面給出了磁性液體密封的設計原則,但對結構參數只給出了經驗的選取范圍,對某一具體結構并沒有細化到其最優值。孫明禮等針對具體結構,在其它條件確定的基礎上,對密封齒形進行了優化設計,這種方法能夠找到特定條件下的最優齒形參數組合,但對整個結構參數的確定來說不夠全面。

　　遺傳算法是基于自然選擇和自然遺傳這種生物進化機制的搜索算法。其對問題的優化過程與生物一代一代的自然進化相類似,它對由多組自變量組成的群體不斷地進行選擇、交叉和變異操作,并按照優勝劣汰的規則,將較優的自變量組合遺傳到下一代,最終在群體中得到最優的自變量組合。遺傳算法具有較高的搜索效率,并能夠減少搜索過程陷于局部最優的風險,且對目標函數幾乎沒有限制,具有較強的適用性 。

　　本文在前人工作的基礎上,采用多目標混合遺傳算法,在保證耐壓指標的約束條件下,對具體密封結構進行優化設計,找到使密封裝置體積最小,成本最低的最優結構參數值。

1、磁性液體密封結構優化的數學模型

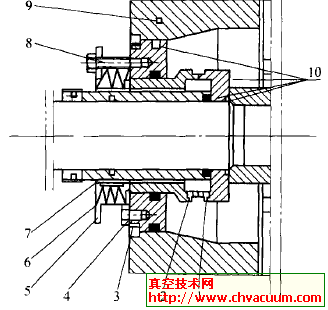
　　密封結構的設計中,在滿足密封耐壓的前提下,人們總是希望設計出體積小、成本低的密封裝置。如圖1 所示的典型磁性液體密封結構中, 軸的半徑r 是由密封對象決定的, 整個裝置總的半徑t 受限于所選擇軸承的外徑, 同時又可根據設計經驗及耐壓指標確定所設計的齒數n 。所以優化設計中以極靴的軸向長度最小和磁鐵的體積最小為目標函數。設計參數分別為:密封間隙lg , 齒寬lt , 槽寬ls , 槽深lh ,磁鐵長度L ,磁鐵寬度s ,磁鐵內徑R 。

圖1 　典型磁性液體密封結構

　　極靴軸向長度的目標函數為

　　磁鐵體積目標函數為

　　根據真空技術網前文中的討論,某一級的密封耐壓值近似為

　　其中μ0 、Ms 、Hmax和Hmin分別為真空磁導率,磁性液體的飽和磁化強度,密封間隙內某一齒下的磁場強度的最大值和最小值。這樣在所有的設計參數下,必須滿足的耐壓條件為

　　其中CP 為給定的耐壓指標。當選定磁性液體后,其飽和磁化強度為定值, 這時密封耐壓值可用各齒下的磁化強度差的極大值來衡量, 所以耐壓條件可以轉變為:

　　式中Hc 為耐壓達到所要求的指標時對應的各齒下的磁化強度差的和的極大值。

　　綜上所述, 并根據磁性液體密封的設計原則 ,可得密封結構優化的數學模型為:

　　式中X = [lg,lt,ls,lh,L,s,R]^T , F 為帶有兩個目標函數的矢量。式中數值的單位為mm。

2、帶約束多目標混合遺傳算法的實現方法

　　本文對密封結構的優化采用目標權重和的遺傳多目標優化方法。該方法是給定每個目標函數的分配權重,然后將加權目標結合為單一目標函數。由于不能明確區分密封結構中極靴軸向長度和磁鐵體積孰重孰輕, 所以在遺傳算法中, 采用隨機權重方法,即起初遺傳搜索向著Pareto 解的前沿進行, 此后隨著進化的進行,適應性地隨機調整權重,這樣可保證群體對搜索方向的多樣性。目標權重和函數為

　　其中, w1 、w2 為權重系數,且w1 、w2 > 0 , w1 + w2 = 1。在優化程序中,隨機權重系數按下式計算:

　　ζ1 ,ζ2 為計算機產生的隨機數。

　　由于密封間隙內磁場只能通過數值方法進行計算,因此我們調用專業的磁場計算軟件Ansys 來實現磁場分布的計算,密封結構模型的建立等操作都通過APDL 編程在Ansys 中完成,完成計算后Ansys將計算結果返回給優化程序。另外,為了增強遺傳算法的局部搜索能力,在遺傳算法中嵌入局部貪婪性搜索過程。為了保證在每一代進化中不遺失較優解,采用定義非受支配解集合的保優策略。總的優化步驟為:

　　(1) 隨機產生M 個初始個體,形成初始群體;

　　(2) 計算各個體的適應度值并調用Ansys 計算磁場分布,對不滿足耐壓條件個體的適應度處以罰函數;

　　(3) 判斷所有個體是否都不滿足耐壓條件,若是,則返回步驟(1)重新產生初始群體;

　　(4) 按適應度大小進行排序,并將適應度最大的前N 個個體存入非受支配解集合;

　　(5) 計算隨機權重系數和除非受支配解外的M-N 個個體在新的權重系數下的適應度;

　　(6) 采用比例選擇的方法進行選擇運算,然后經交叉和變異運算后形成新的群體;

　　(7) 對新群體中的個體及非受支配解集合中的個體執行局部搜索操作得到M 個個體組成的群體;

　　(8) 算法終止判斷,若滿足終止條件,則輸出結果,否則轉到步驟(2)。