活塞式壓力計的基本原理及應用
本文對活塞壓力計的工作原理、結構類型、誤差因素進行了較為詳細的介紹,并結合具體實例,對活塞壓力計的不確定因素進行了定量分析。
壓力(P)不是獨立的基本物理量,而是質量和長度量的導出量。壓力的定義為:
P = F/A (1)
式中,F為力值,A為承受該力值的面積。
根據以上原理,我們可以采用多種方法通過特定的機械裝置產生壓力。其中最常見的方法是液體壓力計裝置和活塞式壓力計裝置。
本文將對活塞式壓力計裝置進行討論。
活塞式壓力計又稱為靜重式壓力計,是利用流體靜力平衡原理及帕斯卡定律工作的儀器。
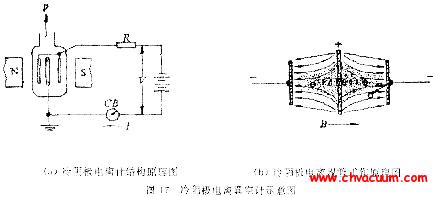
流體靜力平衡是通過作用在活塞系統的力值與傳壓介質產生的反作用力相平衡實現的。活塞系統由活塞和缸體(活塞筒)組成,二者形成極好的動密封配合。活塞的面積(有效面積)是已知的,當已知的力值作用在活塞一端時,活塞另一端的傳壓介質會產生與已知力值大小相等方向相反的力與該力相平衡。由此,可以通過作用力值和活塞的有效面積計算得到系統內傳壓介質的壓力。在實際應用中,力值通常由砝碼的質量乘以使用地點的重力加速度得到。活塞式壓力計的結構類型有很多種。最基本的結構原理如圖1所示。
活塞式壓力計的結構類型有很多種。最基本的結構原理如圖1所示。

由此方法得到的壓力的不確定度取決于儀器本身的物理特性(和不確定度)以及許多外部影響因素。 所有因素都必須予以深入的分析和考慮。對不確定度影響因素的重視程度將直接決定測量結果“誤差”的大小。
來自活塞式壓力計本身的測量不確定度的影響分量主要有:砝碼、活塞系統的剛度、活塞系統的溫度膨脹系數、流體的表面張力、垂直度影響、以及磁場對磁性部件的影響等。 來自外部因素的不確定度影響分量主要有:使用地點的重力加速度、砝碼在空氣中受到的浮力、操作環境的受控程度和穩定程度。應該注意到:我們以上討論的不確定度分量只是局限在活塞壓力計本身的測量不確定度進行分析得出的。如果我們要給出被校驗儀器的測量不確定度報告,還必須對其他因素加以考慮。這些因素包括:與流體介質種類和參考壓力(或氣壓)相關的位置差、系統泄漏、溫度梯度等。
活塞壓力計的結構基本組成
活塞式壓力計的基本組成原理如圖2所示。
從圖2可以看出,活塞壓力計由活塞、活塞筒、基座、砝碼和壓力接口組成。基座對活塞系統起支撐作用并使活塞底部工作面與傳壓介質相接觸,基座底部的螺栓用于調節活塞系統與地面的垂直度。

活塞/活塞筒(活塞系統組件)的類型
對活塞壓力計測量結果影響最大的因素(尤其在高壓力時)是壓力對活塞有效面積的影響。這就是我們通常所說的“壓力形變系數”。基于以上認識,我們通過多種方法對活塞系統組件加以完善,力圖消除或減小“壓力形變系數”對測量結果的影響。
最典型的活塞系統組件有三種結構形式,分別叫做“基本型”、“復入型”和“可控間隙型”。這三種結構形式的活塞系統組件由于其易實現性和商業上的可行性,至今仍被廣泛采用。
基本型:基本型是所有活塞系統類型中最簡單的一種結構。其結構原理如圖 2 所示。基本型結構中,活塞筒的外表面始終暴露在大氣中。活塞筒的直徑會隨著壓力的增加而增大,從而導致活塞有效面積的增大,為“正”壓力變形系數。
復入型 :如圖3 所示。在這種結構類型中,將活塞系統內部壓力施加到活塞筒外表面的一部分。這樣以來,當系統壓力增加時,活塞的有效面積通常會減小,為“負”壓力變形系數。
可控間隙型: 在這種結構類型中,活塞和活塞筒之間的間隙由作用在活塞筒外部(參與工作部分)的獨立壓力控制系統進行控制。目的是消除壓力變形系數,使得活塞的有效面積不隨系統試驗壓力的改變而變化。其結構原理圖如圖4 所示。

壓力與力值的關系 基本因素
影響壓力與力值關系的基本因素有:浮力、重力加速度、流體表面張力系數,以及溫度系數引起的線性膨脹、壓力系數引起的彈性變形對活塞有效面積的影響等。
由壓力的基本定義:
Pr=F/Ac (2)
式中:
Pr --- 活塞工作端面壓力值
F --- 作用在活塞上的力值(砝碼重力)
Ae --- 活塞系統有效面積
又由,
F = Ma · g1 (3)
得到:
Pr=Ma ·g1/Ac (4)
式中:
Ma = 砝碼質量(經標準檢定給出的表觀值,包括活塞及連接件質量)。
gl = 使用地點重力加速度。
力值修正
浮力影響
根據阿基米德定律: 物體受到的浮力等于物體排開的流體的重量。物體在空氣中的重量要小于物體在真空環境中的重量,減少的重量等于物體排開的空氣的重量,近似等于空氣的密度乘以物體的體積。對于形狀不規則的物體,體積很難通過幾何測量的方法計算得到,即便可以通過計算得到,還需要知道該物體材料的密度。如果物體的質量是以表觀值表示而不是以真實質量表示的,則在進行浮力修正時,只要知道稱量該物體質量時所使用的標準砝碼的密度就可以了。這種方法已被普遍接受,并使得浮力影響修正得以簡化。
在對表觀值表示質量的砝碼進行浮力修正時,可以不必知道砝碼的密度,而直接通過稱量該物體質量時所使用的標準砝碼的密度進行修正(可推導證明)。盡管這樣會引入很小的誤差,但對于活塞壓力計的浮力修正很實用,且不會造成明顯的誤差。
浮力修正公式為:
1-ρa/ρs (5)
式中:
ρa = 砝碼周圍空氣的密度
ρs = 上級標準砝碼的密度