針對由電機慣性造成的電動執行器不能精確定位的問題，介紹了一種新的電動執行器控制算法--貼近算法，并對基于該算法的電動執行器進行了仿真分析。不同于傳統的電動執行器，基于貼近算法的電動執行器不需要任何制動裝置就能有效地利用電機的慣性準確定位。詳細描述了貼近算法，利用Matlab編程實現了該算法，最后對電動執行器進行仿真試驗。仿真結果驗證了貼近算法的可行性、有效性及局限性。

1、引言

　　電動執行器作為工業自動控制系統中的執行元件，要求對系統發出的指令做出快速、準確的反應，以確保系統的正常運行。針對電動執行器，目前主要著重研究的是控制算法、電機的驅動方式和制動方式。隨著現場總線廣泛應用于工業控制中，基于現場總線的智能執行器也是目前研究的一個方向。

　　為了解決由于電機的慣性而引起電動執行器惰走的問題，目前常用的方法是采用機械制動或電氣制動來克服電機的慣性。雖然抱閘裝置或電磁設備能使電機快速停轉，但是電動執行器的結構也因此變得異常復雜，同時其精確度也隨著制動裝置的機械磨損而受到影響。而貼近算法，是基于利用電機慣性使電動執行器準確定位的基本思想。通過對基于貼近算法的電動執行器進行仿真試驗，分析得出貼近算法的控制效果取決于電機的轉動慣量和貼近算法的參數。在一定的條件下，基于貼近算法的電動執行器能夠快速準確地定位。

2、電動執行器的結構

　　電動執行器主要由控制單元、電機和執行機構組成，其基本原理如圖1所示。控制單元根據給定信號與調節機構位移反饋量的偏差產生控制量驅動電機運行，經過變速及傳動裝置輸出角位移或直行程位移，實現對閥門、擋板等調節機構的位置控制。

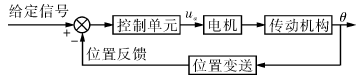
圖1 電動執行器原理框圖

　　電動執行器的機理模型可簡化為：

　　式中：θ--電動執行器的角位移輸出;ua--控制單元的輸出。

　　式中：J--電機總等效轉動慣量;f--電機總等效粘性摩擦系數;CM--阻尼系數;Z1--電機主動齒輪齒數;Z2--電機從動齒輪齒數;M3--電機從動齒輪的負載力矩。

3、貼近算法

　　基于貼近算法的電動執行器不需要制動裝置克服電機的慣性。位置反饋信號與給定信號的偏差為ek=sp–y。當ek達到事先設定的閾值時，電動執行器的電機斷電，電機轉子在慣性的作用下，帶動調節機構達到設定值。

3.1、貼近算法的基本思想

　　首先為電動執行器的位置反饋值與給定值之間的偏差ek設定兩個死區閾值：外死區閾值α和內死區閾值β，如圖2所示。

　　當偏差絕對值大于α時，給電機通正向或反向電壓;當偏差的絕對值介于α和β之間時，切斷電機電源，電機轉子在慣性作用下轉動。內死區閾值β與精度相關，當偏差絕對值小于β時，可認為電動執行器已經達到了精度要求。控制算法的輸出量uk的取值為0、1、-1，分別表示電機斷電、施加正向電壓、施加反向電壓。

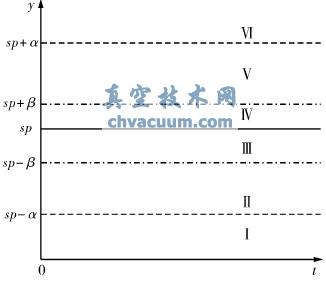
圖2 外死區閾值α和內死區閾值β

3.2、貼近算法的具體描述

　　(1)當ek≥α時，執行器輸出y進入區域I，即調節機構的位置還沒達到設定的外死區閾值。則電機應該正轉，需要給電機施加正向電壓，即貼近算法的輸出uk=1。

　　(2)當β≤ek<α時，執行器輸出y進入區域II，即內、外死區之間。對此分兩種情況討論：

　　①果上一采樣周期的控制算法輸出uk-1=1且偏差ek-1≥α，執行器輸出y在前一個的采樣周期剛從區域I進入區域II，此時應切斷電機的電源，即uk=0，使轉子在慣性的作用下繼續轉動。但是如果uk-1=1且β≤ek-1<α，說明執行器輸出y在上一采樣周期之前就已經進入了區域II，但在慣性作用下仍然沒有到達內死區，因此需要繼續給電機施加正向電壓，uk=1。

　　②另一種情況是，如果上一采樣周期的輸出uk-1=0，說明在上一個采樣周期中，轉子已經在慣性作用下轉動了。在這種情況下就應判斷電機轉子是否已經停止。若ek≠ek-1，說明電機轉子還沒停止轉動，所以算法的輸出uk=0，讓電機繼續在慣性作用下轉動。如果ek=ek-1，說明電機轉子已經停止，那么繼續給電機施加正向電壓，即uk=1;

　　(3)當0≤ek<β時，執行器輸出y在區域III，達到精度要求，應切斷電機電源，即uk=0。

　　(4)當ek<-α時，執行器輸出y在區域VI，電機應該反轉，使y減小，所以應給電機施加反向電壓，即uk=-1。

　　(5)當-α≤ek<-β時，這與β≤ek<α的情況類似，考慮兩種情況：

　　①當uk-1=-1且偏差為ek-1≤-α時，執行器輸出y剛從區域。進入區域。，應使電機斷電，即uk=0，使轉子利用慣性轉動。如果uk-1=-1且-α≤ek-1<-β，說明執行器輸出y在慣性作用下還沒到達內死區內，此時電機應該反轉，即uk=-1。

　　②當uk-1=0時，說明在上一個采樣周期中電機已經斷電，在這種情況下就應判斷電機轉子在慣性作用下的轉動是否已經停止。若ek≠ek-1，說明電機轉子還沒停止，應使電機繼續在慣性作用下轉動，所以算法的輸出uk=0。如果ek=ek-1，說明電機轉子已經停止，但執行器輸出y還沒到達內死區，那么需要再給電機加反向電壓，即uk=-1。

　　(6)當-β≤ek≤0，執行器輸出y在區域。，執行器輸出y已達到精度要求，使電機斷電，uk=0。

3.3、貼近算法的數學描述

　　將上述對貼近算法的文字描述表示為如式(4)所示的數學表達式：

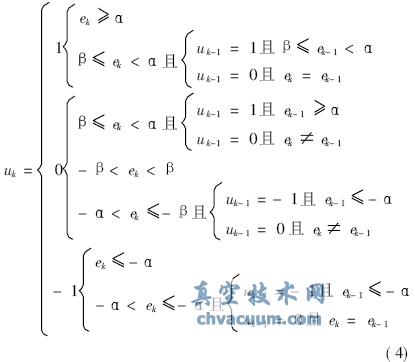
4、仿真實例

　　根據表達式(4)，利用Matlab編程實現貼近算法，并分別在單位階躍和正弦輸入下對電動執行器進行仿真。

4.1、電動執行器的單位階躍響應

　　根據式(2)和式(3)可知，k和τ的值與電機的轉動慣量J成反比。因此選取兩組k和τ的值，在單位階躍輸入下對電動執行器進行仿真。兩組k和τ的值分別為：k=0.012，τ=0.5;k=0.0012，τ=0.05。貼近算法中的參數：外死區閾值和內死區閾值設為α=0.005，β=0.003。電動執行器單位階躍響應曲線如圖3所示。

　　圖3說明當電機慣量大小合適時，采用貼近算法的電動執行器能快速、準確地定位。但是當電機的轉動慣量增大時，電動執行器單位階躍響應的超調量增加，調節時間變長。若電機轉動慣量太大，電動執行器會發生振蕩。這是因為電機慣性太大，使電機轉子在慣性的作用下轉角太大，當內、外死區閾值之差很小時，偏差的絕對值∣ek∣總是大于外死區閾值A，致使電動執行器不能在電機慣性的作用下達到設定值。

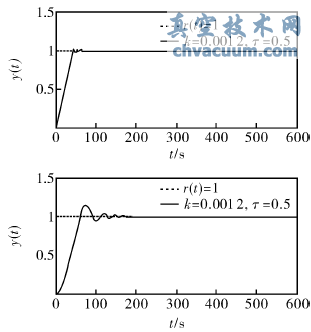
圖3 不同轉動慣量的電動執行器單位階躍響應

　　鑒于轉動慣量太大的問題，通過改變外死區閾值α，對電機參數為k=0.0012，τ=0.05的電動執行器進行仿真，得到外死區閾值α=0.005和α=0.03時電動執行器的單位階躍響應曲線如圖4所示。

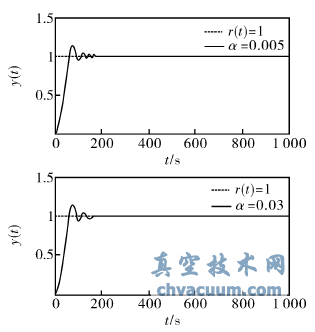
圖4 選取不同外死區閾值的電動執行器單位階躍響應

　　由圖4可知，當外死區α從0.005增加到0.03后，電動執行器調節時間變短，收斂速度加快，但是超調量沒有減小。

4.2、電動執行器的正弦響應

　　為了驗證基于貼近算法的電動執行器對時變輸入的響應，在正弦輸入下對電動執行器進行仿真。

　　選取三組電機參數：k=0.012，τ=0.5;k=0.0012，τ=0.05;k=0.00012，τ=0.005。貼近算法中的參數：外死區閾值和內死區閾值設為α=0.005，β=0.003。電動執行器的正弦響應曲線如圖5所示。

　　由圖5可知，在電機轉動慣量較小時，基于貼近算法的電動執行器能迅速準確地定位，跟蹤時變輸入信號。但當電機的轉動慣量過大時，電動執行器在慣性的作用下偏離設定值，使偏差過大，超過外死區閾值，從而電動執行器不能利用電機的慣性準確地定位。

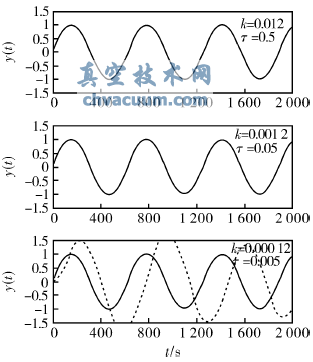
圖5 不同轉動慣量的電動執行器正弦響應

　　改變外死區閾值α對電動執行器進行仿真，得到外死區閾值分別α=0.005和α=0.03時電動執行器的正弦響應曲線如圖6所示。

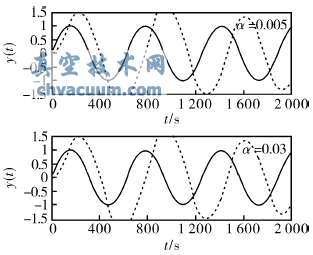
圖6 改變外死區設定值時電動執行器的正弦響應

　　由圖6可知，改變外死區閾值對仿真結果的影響不明顯，說明貼近算法對于時變的輸入信號的跟蹤能力主要取決于電機的轉動慣量。

5、結論

　　針對電動執行器制動裝置對電動執行器結構和性能的影響，為了簡化電動執行器的結構，同時提高其定位的準確性，研究了貼近算法在電動執行器中的應用。采用該算法的電動執行器不需要制動裝置。通過對偏差設置內死區閾值和外死區閾值，使電動執行器在電機慣性的微調作用下準確定位。通過仿真試驗得出結論：如果選擇合適的電機轉動慣量和外死區閾值，基于貼近算法的電動執行器能實現準確快速地定位。但是，對于時變的輸入信號，在電機轉動慣量太大的情況下，即使調整外死區閾值的大小，仍然無法使電動執行器準確定位。因此，如何改善基于貼近算法的電動執行器對時變輸入的跟蹤性能將是下一步的研究方向。